Số hữu tỉ là một phần không thể thiếu trong môn Toán học. Vì vậy, trong bài viết hôm nay sẽ cung cấp cho các em học sinh đầu đủ những kiến thức liên quan đến phần này! Hãy cùng theo dõi nhé!
Định nghĩa số hữu tỉ là gì?
Số hữu tỉ là các số có thể biểu diễn được dưới dạng phân số (thương) (a/b). Trong đó, a và b là các số nguyên với điều kiện b≠a.
Tập hợp số hữu tỉ là tập hợp có thể đếm được.
Các số thực không phải là số hữu tỉ thì được gọi là các số vô tỉ.
Tuy nhiên, tập hợp của các số hữu tỉ không hoàn toàn đồng nhất với tập hợp các phân số 
. Bởi vì mỗi số hữu tỉ có thể biểu diễn bằng nhiều phân số khác nhau. Chẳng hạn các phân số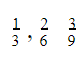 
… đều cùng biểu diễn một số hữu tỉ. Tập hợp số hữu tỉ được kí hiệu là Q trong đó:
Q = a,b∈Z và b≠0
Khái niệm số hữu tỉ
Tính chất số hữu tỉ là gì?
Sau khi tìm hiểu về định nghĩa của số hữu tỉ. Chúng ta hãy cùng tìm hiểu tính chất của số hữu tỉ như sau:
Nhân số hữu tỉ
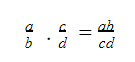
Ví dụ:
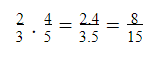
Chia số hữu tỉ
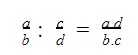
Ví dụ:
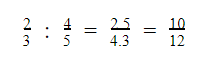
Mỗi số hữu tỉ đều có thể biểu diễn bằng một số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Giá trị tuyệt đối của các số hữu tỉ
|x| = x nếu x≥0
|x| = -x nếu x<0
Số hữu tỉ gồm có những tính chất gì?
Số đối của số hữu tỉ
- Số đối của số hữu tỉ là một số hữu tỉ mà tổng của nó với số hữu tỉ này cho kết quả bằng 0.
- Nếu số hữu tỉ là số hữu tỉ âm thì số đối của nó sẽ là số hữu tỉ dương.
- Nếu số hữu tỉ là số hữu tỉ dương thì số đối của nó là một số hữu tỉ âm.
- Lũy thừa của một số hữu tỉ số bằng tích của các lũy thừa.
- Lũy thừa của một tích sẽ bằng tích của các lũy thừa:
- Lũy thừa của một thương bằng thương của các lũy thừa:
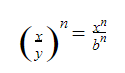
Bài tập về các số hữu tỉ
Để củng cố thêm kiến thức về số hữu tỉ, các bạn hãy cùng chuthapdoquangninh.org.vn cùng giải quyết một số bài tập sau đây nhé!
Bài tập 1
Tìm x biết x∉{1;3;8;20}
và: 2(x−1)(x−3)+5(x−3)(x−8)+12(x−8)(x−20)−1x−20=−34.
Giải:
Ta có: 2(x−1)(x−3)+5(x−3)(x−8)+12(x−8)(x−20)−1x−20
=(x−1)−(x−3)(x−3).(x−1)+(x−3)−(x−8)(x−8).(x−3)+(x−8)−(x−20)(x−20).(x−8)−1x−20.
=1x−3−1x−1+1x−8−1x−3+1x−20−1x−8−−1x−20=−1x−1.
⇒−1x−1=−34⇒x=73.
Bài tập về số hữu tỉ
Bài tập 2
Tìm x∈Q biết: (23x−15)(35x+23)<0.
Giải:
Ta có: (23x−15)(35x+23)<0
⇔[23(x−310)][35(x+109)]<0
⇔23.35(x−310)(x+910)<0
⇔(x−310)(x+109)<0
Từ đó suy ra: x−310 và x+109 trái dấu, mặt khác ta lại có x−310<x+109
Nên suy ra: x−310<0 và x+109>0⇔−109<x<310.
Vậy các số hữu tỉ x thỏa mãn đề ra là −109<x<310.
Bài tập 3
Viết 5 số hữu tỉ trên một vòng tròn sao cho trong đó tích hai số cạnh nhau bằng 136. Hãy tìm cách viết đó.
Giải:
Gọi 5 số hữu tỉ đó lần lượt là a1, a2, a3, a4, a5 (các số này đều khác 0)
Ta có: a1a2=a2a3⇒a1=a3
Tương tự có: a2=a4,a3=a5
Mà: a1a2=a5a1⇒a2=a5.
⇒a1=a2=a3=a4=a5=±16.
Bài tập nâng cao phần số hữu tỉ
Bài tập 4
- a) Cho 13 số hữu tỉ, trong đó tổng của bốn số bất kì đều là một số dương. Chứng minh rằng tổng của 13 số đó cũng là một số dương.
- b) Cho 13 số hữu tỉ, trong đó tích của 3 số bất kì đều là một số âm. Chứng minh rằng 13 số đã cho trên đều là số âm.
Giải:
Giả sử 13 số đã cho lần lượt là: a1;a2;a3;…;a12;a13.
- a) Ta xét 13 tổng sau: a1+a2+a3+a4>0
a2+a3+a4+a5>0
a3+a4+a5+a6>0
…..
a13+a1+a2+a3>0.
Cộng các bất đẳng thức trên vế theo vế ta có : 4(a1+a2+a3+…+a13)>0.
⇒a1+a2+a3+…+a13>0
Vậy tổng của 13 số đã cho đều là một số dương.
- b) Xét 13 tích: a1.a2.a3<0,a2.a3.a4<0,…,a13.a1.a2<0.
=> (a1.a2.a3…a13)3<0⇒a1.a2.a3…a13<0.
Tách riêng một số từ tích 13 số nêu trên, 12 số còn lại chia thành 4 nhóm ba số ta có:
(a1.a2.a3).(a4.a5.a6).(a7.a8.a9).(a10.a11.a12).a13<0.
Ta thấy tích mỗi nhóm ba số trên là một số âm nên tích của 4 nhóm như vậy là số dương. Từ đó suy ra số được tách riêng ra là một số âm.
Tương tự cho 13 số và ta được 13 số đã cho đều là một số âm.
Trên đây là những kiến thức và bài tập liên quan đến phần số hữu tỉ. Hy vọng với những gì mà chuthapdoquangninh.org.vn chia sẻ sẽ giúp được các bạn học sinh bổ sung thêm kiến thức ở phần này. Cảm ơn các bạn đã quan tâm theo dõi, hẹn gặp lại ở những bài tiếp theo nhé!
Xem thêm:
- Công thức tính diện tích xung quanh hình hộp chữ nhật
- Hướng dẫn cách tính diện tích hình tròn, hình quạt tròn
- Số thực là gì? Số thực bao gồm những số nào?
- Cách tính chu vi tam giác đầy đủ và chi tiết nhất
- Số chính phương là gì? – Định nghĩa, tính chất và bài tập áp dụng
