“Trọng tâm là gì? Đường trung tuyến là gì?” là những câu hỏi được nhiều học sinh quan tâm bởi rất quan trọng trong Toán Hình học. Vậy nên bài viết này, chúng tôi sẽ đưa ra định nghĩa, tính chất và cách vẽ để các bạn nắm vững kiến thức này.
Trọng tâm là gì?
Khái niệm
Trọng tâm của một vật thể là một điểm mà khi đặt trụ thẳng đứng vào điểm đó thì vật thể có thể đứng cân bằng được.
Trọng tâm của tam giác chính là giao điểm của ba đường trung tuyến trong tam giác đó. Vậy đường trung tuyến là gì? Chúng ta sẽ cùng tìm hiểu chi tiết ở phần sau nhé.
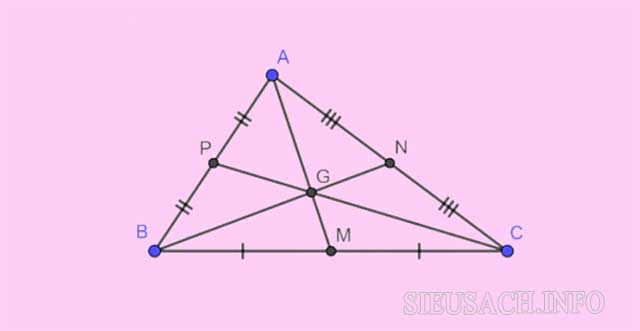
Trọng tâm của tam giác chính là giao điểm của ba đường trung tuyến trong tam giác
Tính chất trọng tâm trong tam giác
Sau khi tìm hiểu rõ trọng tâm là gì ở bên trên, chúng ta sẽ cùng tìm hiểu chi tiết về tính chất của trọng tâm tam giác trong phần này. Cụ thể như sau:
– Trong tam giác thường: Khoảng cách từ trọng tâm của tam giác đến đỉnh luôn bằng 2/3 độ dài của đường trung tuyến ứng với đỉnh đó.
Ví dụ: Cho tam giác ABC, với các đường trung tuyến lần lượt là AM, BN, CP và trọng tâm G. theo tính chất thì ta có:

– Trong tam giác vuông: Trọng tâm cũng được xác định giống như trọng tâm của tam giác thường.
Ví dụ: Cho tam giác MNP vuông tại M, có 3 đường trung tuyến MD, NE và PF giao nhau tại trọng tâm O. Ta có MD lại là đường trung tuyến của góc vuông PMN nên => MD = 1/2 PN = DP = DN.
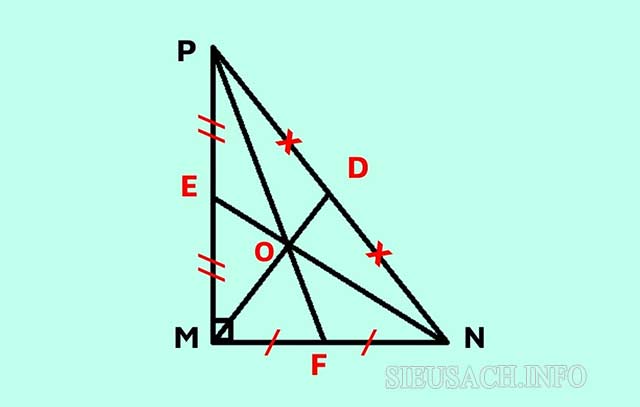
Tính chất trọng tâm của tam giác vuông MNP
– Tam giác cân: Cho tam giác ABC cân tại đỉnh A, có G là trọng tâm.
Vì tam giác ABC cân tại đỉnh A nên AG vừa là đường trung tuyến, đường cao và cũng là đường phân giác.
=> Hệ quả trọng tâm của tam giác cân ABC như sau:
+ Góc BAD = góc CAD. (D là trung điểm của BC)
+ Đường trung tuyến AD sẽ vuông góc với cạnh đáy BC.
– Tam giác vuông cân: Có tam giác ABC vuông cân tại đỉnh A, I là trọng tâm. AM vừa là đường trung trực, vừa đường trung tuyến và đường cao của tam giác này nên AM sẽ vuông góc với BC.
Mặt khác, tam giác ABC vuông cân tại A nên ta có AB = AC.
Suy ra:
+ BP = CN
+ BN = AN = CP = AP.
– Tam giác đều: Cho tam giác ABC đều, G chính là giao điểm của ba đường trung tuyến, đường cao và đường phân giác. Theo tính chất của tam giác đều ta có điểm G vừa là trọng tâm, trực tâm, vừa là tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.
Cách tìm trọng tâm tam giác chuẩn xác
Cách 1: Là giao điểm của 3 đường trung tuyến
– Bước 1: Các bạn vẽ tam giác ABC rồi lần lượt xác định trung điểm E, G, F của các cạnh AB, BC và CA.
– Bước 2: Nối lần lượt các đỉnh và trung điểm của cạnh đối diện. Nối A với G, B với F và C với E.
– Bước 3: Giao điểm I của ba đường trung tuyến AG, BF và CE chính là trọng tâm của tam giác ABC.
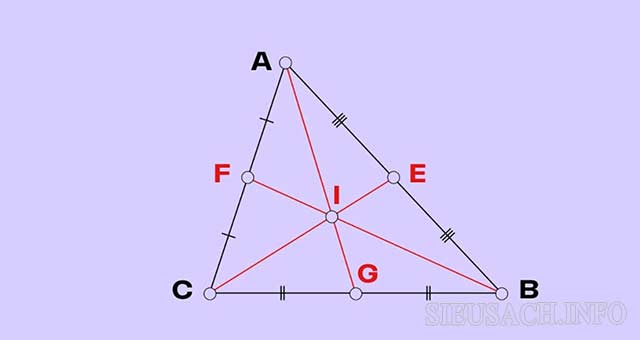
Cách tìm trọng tâm tam giác bằng 3 đường trung tuyến
Cách 2: Tỉ lệ ở trên đường trung tuyến
– Bước 1: Vẽ tam giác ABC rồi xác định trung điểm M của cạnh BC.
– Bước 2: Nối đỉnh A với trung điểm M rồi sau đó lấy điểm S trên AM sao cho AS = 2/3 AM.
Theo tính chất trọng tâm của tam giác thì điểm S chính là trọng tâm của tam giác ABC.
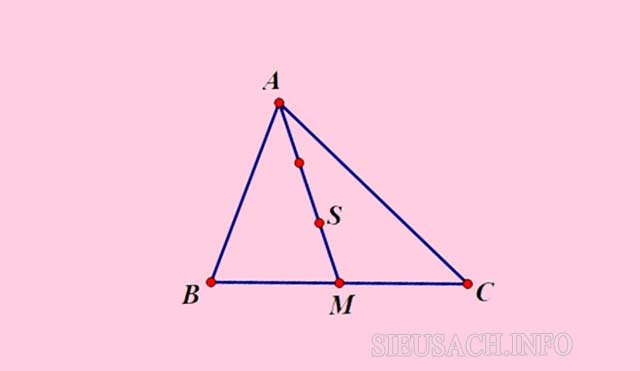
Cách tìm trọng tâm của tam giác bằng độ dài của đường trung tuyến
Đường trung tuyến là gì?
Sau khi đã hiểu rõ trọng tâm là gì ở bên trên, chúng ta sẽ cùng tìm hiểu chi tiết về đường trung tuyến. Mời các bạn cùng theo dõi!
Định nghĩa đường trung tuyến
Đường trung tuyến của một đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng đó.
Đường trung tuyến trong tam giác chính là đoạn thẳng nối từ đỉnh của tam giác đến trung điểm của cạnh đối diện, mỗi tam giác sẽ có 3 đường trung tuyến.
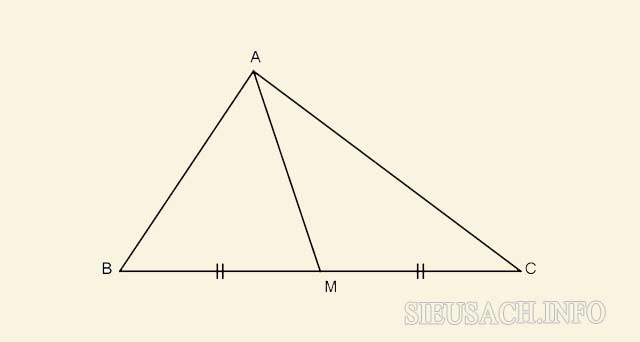
Đường thẳng AM là đường trung tuyến của tam giác ABC
Tính chất đường trung tuyến trong tam giác
Khi đã hiểu rõ về khái niệm đường trung tuyến là gì, trọng tâm là gì, chúng ta sẽ cùng tìm hiểu về tính chất của đường trung tuyến ở dưới đây:
– Tính chất đường trung tuyến trong tam giác thường:
Ba đường trung tuyến của tam giác sẽ cùng đi qua một điểm và điểm đó cách đỉnh của tam giác một khoảng bằng 2/3 độ dài của đường trung tuyến đi qua đỉnh ấy. Giao điểm này thường được gọi là trọng tâm.
– Tính chất đường trung tuyến trong tam giác vuông:
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền sẽ bằng 1/2 cạnh huyền. Đường trung tuyến của tam giác vuông cũng có đầy đủ các tính chất giống một đường trung tuyến của tam giác thường.
Giả sử: Tam giác ABC vuông có AD là trung tuyến ứng với cạnh huyền BC.
=> AD = 1/2BC = DB = DC
Ngược lại, nếu trung tuyến AD = 1/2BC thì ABC vuông tại đỉnh A.
– Tính chất đường trung tuyến trong tam giác cân:
Đường trung tuyến ứng với cạnh đáy của tam giá cân thì vuông góc với cạnh đáy và chia tam giác thành 2 tam giác con bằng nhau.
Giả sử: Tam giác ABC cân tại đỉnh A, có đường trung tuyến AD ứng với cạnh đáy BC.
Suy ra:
AD vuông góc với cạnh BC
ΔADB = ΔADC
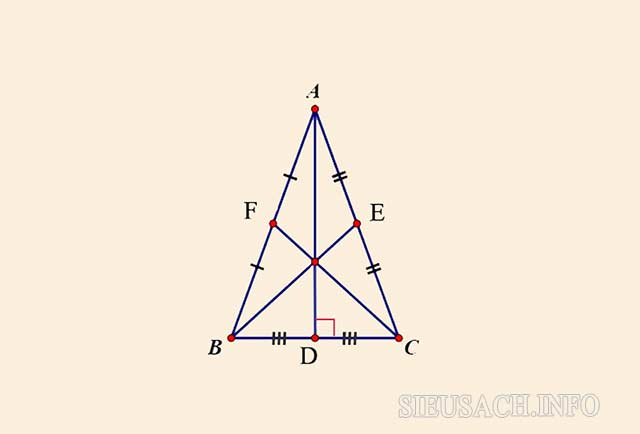
Đường trung tuyến AD, BE và CF trong tam giác cân ABC
– Tính chất đường trung tuyến trong tam giác đều:
3 đường trung tuyến của tam giác đều sẽ chia tam giác đó thành 6 tam giác con có diện tích bằng nhau. Trong tam giác đều, đường thẳng đi qua một đỉnh bất kỳ và trọng tâm của tam giác đó sẽ chia tam giác thành 2 tam giác con có diện tích bằng nhau.
Giả sử: Tam giác ΔABC đều. Trung điểm của các cạnh BC, AB và AC lần lượt là D, E, F. Điểm G là trọng tâm của tam giác ABC.
Suy ra:
ΔGAE = ΔGCF = ΔGAF = ΔGCD = ΔGBE = ΔGBD = ΔGEB = ΔGEA
SADB = SADC = SCEA = SCEB = SBFA = SBFC
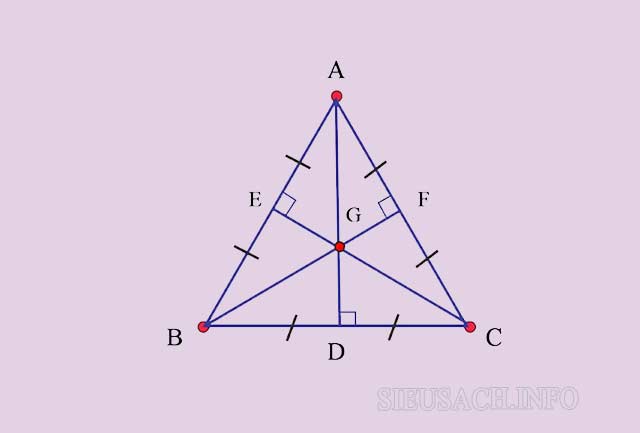
Tính chất của đường trung tuyến AD, BF và CE trong tam giác đều ABC
Công thức tính độ dài đường trung tuyến của tam giác
Sau khi đã hiểu rõ định nghĩa trọng tâm là gì, đường trung tuyến là gì, chúng ta sẽ cùng tìm hiểu về cách tính đường trung tuyến trong tam giác chuẩn xác. Độ dài của đường trung tuyến tam giác được tính thông qua độ dài của các cạnh trong tam giác và được tính bằng định lý Apollonnius theo công thức:
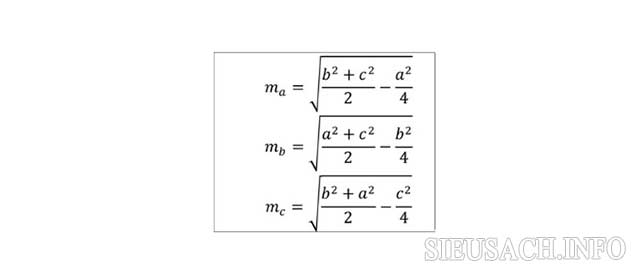
Trong đó:
– a, b, c: là độ dài các cạnh của tam giác đã cho.
– ma, mb, mc: là các đường trung tuyến tương ứng với các đỉnh của tam giác.
Các dạng bài tập về đường trung tuyến trong tam giác
Dạng 1: Sử dụng tính chất trọng tâm tam giác
Phương pháp giải:
- 3 đường trung tuyến của tam giác đồng quy tại một điểm. điểm này gọi là trọng tâm của tam giác
- Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy
Dạng 2: Chứng minh một điểm là trọng tâm tam giác
Phương pháp giải: Sử dụng tính chất trọng tâm của tam giác
Dạng 3: Đường trung tuyến của tam giác cân, tam giác đều, tam giác vuông
Phương pháp giải: Chú ý đến tính chất của tam giác cân, tam giác đều và tam giác vuông.
Bài tập về trọng tâm và đường trung tuyến tam giác
Với các thông tin trọng tâm là gì, đường trung tuyến là gì ở bên trên, chắc chắn các bạn đã phần nào hiểu rõ hơn. Để củng cố kiến thức vững chắc, chúng tôi sẽ chia sẻ cho các bạn những bài tập rèn luyện ở bên dưới đây.
Bài 1: Cho tam giác ABC có đường trung tuyến AD = 9cm và trọng tâm I. Tính độ dài của đoạn AI?
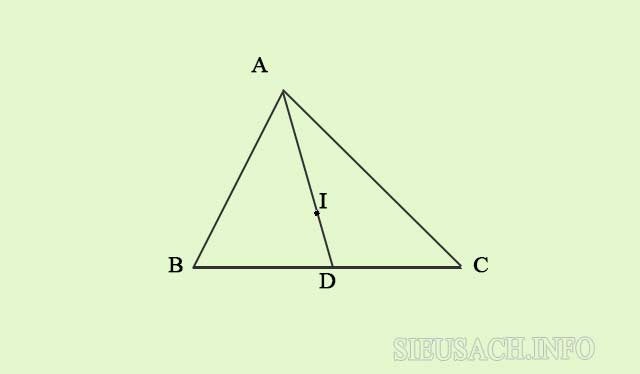
Hình minh họa bài tập 1
Lời giải:
Ta có: – Điểm I là trọng tâm của tam giác ABC.
– AD là đường trung tuyến.
=> AI = (2/3) AD (theo tính chất ba đường trung tuyến của tam giác ở bên trên).
Do đó: AG = (2/3).9 = 6 (cm).
Vậy đọan AI cần tìm có độ dài 6 cm.
Bài 2:
Cho điểm I là trọng tâm của tam giác đều MNP. Hãy chứng minh rằng: IM = IN = IP.
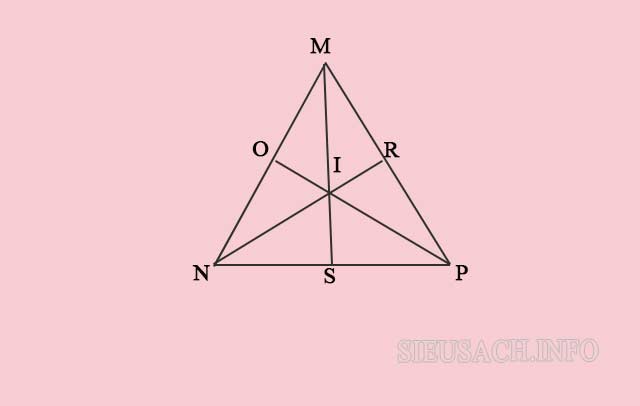
Hình minh họa bài tập 2
Lời giải:
Gọi trung điểm của các cạnh MN, MP và PN lần lượt là R, O, S. Khi đó, các đường trung tuyến MS, PR, NO sẽ đồng quy tại trọng tâm I.
Ta có tam giác MNP đều, suy ra:
MS = PR = NO (1).
Vì I là trọng tâm của tam giác MNP nên theo tính chất của đường trung tuyến ta có:
MI = 2/3 MS, PI = 2/3 PR và NI = 2/3 NO (2).
Từ (1) và (2) ⇒ IM = IN = IP.
Bài 3: Cho tam giác ABC có hai đường trung tuyến BD, CE cắt nhau tại G. Trên tia đối của tia DB lấy điểm M sao cho DM = DG. Trên tia đối của tia EG lấy điểm N sao cho EN = EG Chứng minh rằng:
a) BG = GM; CG = GN
b) MN = BC và MN //BC
Giải:
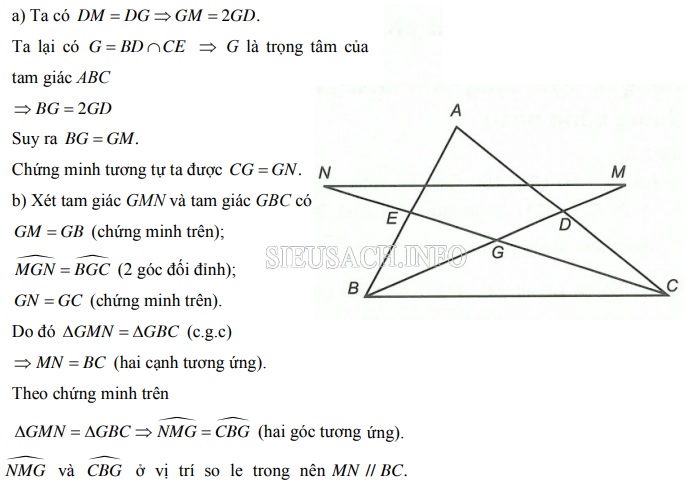
Bài 4: Cho tam giác ABC, D là trung điểm của AC. Trên đoạn BD lấy điểm E sao cho BE = 2ED . Điểm F thuộc tia đối của tia DE sao cho BF = 2BE. Gọi K là trung điểm của CF và G là giao điểm của EK với AC.
a) Chứng minh G là trọng tâm tam giác EFC.
b) Tính các tỉ số .
– GE / GC
– GK / DC
Giải:
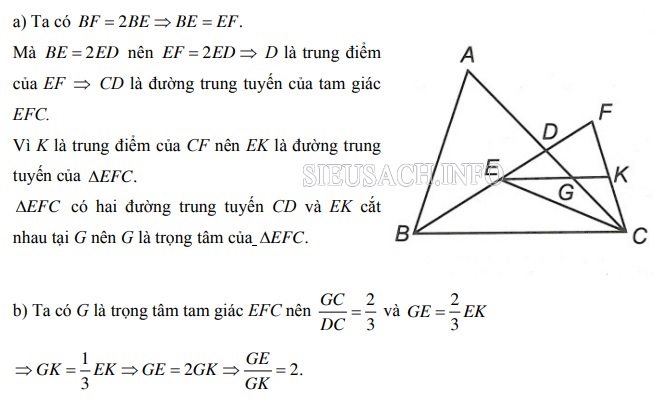
Bài 5:
Hy vọng bài viết này mang đến những kiến thức hình học hữu ích để các bạn nắm rõ trọng tâm là gì, đường trung tuyến là gì. Từ đó áp dụng vào làm bài tập, bài kiểm tra và bài thi được tốt nhất.




