Định lý Talet là một định lý về tỷ lệ, nó rất quan trọng trong môn hình học và cũng là kiến thức nền tảng cho nhiều kiến thức sau của môn toán hình học lớp 8. Cùng chúng tôi tìm hiểu kỹ hơn về định lý Talet trong bài viết này nhé.
Tỉ số của hai đoạn thẳng là gì?
Trước khi tìm hiểu về định lý Talet, chúng ta hãy cùng nhắc qua về tỉ số của hai đoạn thẳng:
Tỉ số của 2 đoạn thẳng chính là tỉ số độ dài của chúng theo cùng một đơn vị đo. Tỉ số của 2 đoạn thẳng không phụ thuộc vào cách chúng ta chọn đơn vị đo.
Tỉ số của 2 đoạn thẳng AH và BE được kí hiệu là AH/BE.
Ví dụ sau: Cho đoạn thẳng AB và 1 tỉ số m/n > 0. Điểm C thuộc AB, ta đã biết CA/CB = m/n. Khi đó, ta gọi điểm C chính là điểm chia đoạn thẳng AB theo tỉ số m/n.
Đoạn thẳng tỉ lệ
Giả sử chúng ta có 2 đoạn thẳng là AB và CD. Hai đoạn thẳng này tỉ lệ với 2 đoạn thẳng A’B’ và C’D’ nếu như có tỉ lệ thức: AB/CD = A’B’/C’D’ hoặc AB/A’B’ = CD/C’D’.

Đoạn thẳng tỷ lệ
Định lý Talet trong tam giác
Định lý Talet thuận
Định lý Talet thuận được phát biểu như sau: Nếu như có một đường thẳng cắt hai cạnh của một tam giác và nó song song với cạnh còn lại thì sẽ định ra trên hai cạnh đó các đoạn thẳng tương ứng với tỉ lệ.
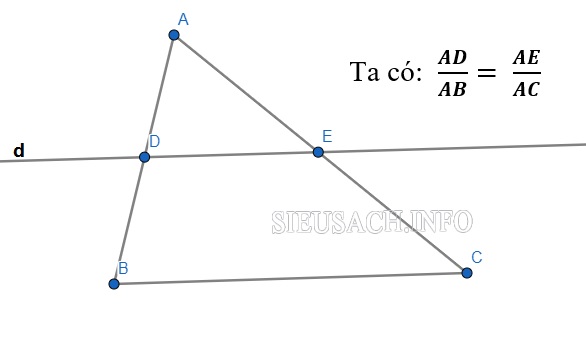
Định lý Talet trong tam giác
Ví dụ: Cho tam giác ABC, đường thẳng d cắt AB ở D, cắt AC ở E và song song với BC.
Theo định lý Talet, ta có:
AB’/AB = AC’/AC
Định lý Talet đảo
Định lý Talet đảo được phát biểu như sau: Nếu một đường thẳng cắt hai cạnh của một tam giác và nó định ra trên hai cạnh này những đoạn thẳng tương ứng với tỉ lệ thì đường thẳng đó sẽ song song với cạnh còn lại của tam giác.
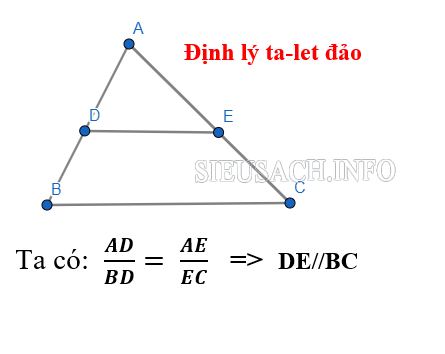
Định lý Talet đảo
Lưu ý: Định lý vẫn đúng trong trường hợp đường thẳng cắt phần kéo dài hai cạnh của một tam giác.
Ví dụ: Trong △ABC, ta sẽ có B’C’ // BC. Định lý Talet thuận và định lý Talet đảo có thể áp dụng được đối với 3 trường hợp hình vẽ như sau:
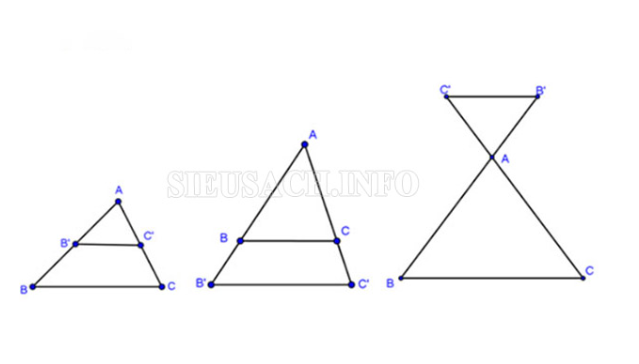
3 trường hợp áp dụng định lý Talet thuận – đảo
Hệ quả của định lý Talet
Hệ quả 1
Hệ quả đầu tiên của định lí Talet trong tam giác đã được phát biểu như sau: Khi một đường thẳng song song với một cạnh của một tam giác cho sẵn, đồng thời cắt 2 cạnh còn lại thì sẽ tạo ra một tam giác mới với ba cạnh tỉ lệ với ba cạnh của tam giác đã cho trước.
Trong △ABC, đường thẳng DE // BC thì chúng ta sẽ có:
AD/AB = AE/AC = DE/BC
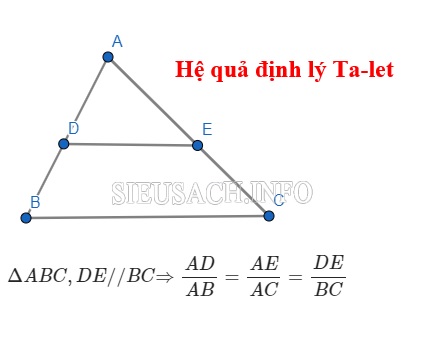
Hệ quả định lý Talet
Đặc biệt, hệ quả 1 vẫn đúng trong trường hợp có một đường thẳng a song song với 1 cạnh của tam giác đã cho và nó cắt 2 cạnh còn lại của tam giác khi kéo dài.
Hệ quả 2
Hệ quả 2 của định lý Talet như sau: Khi một đường thẳng cắt ngang 2 cạnh của một tam giác đã cho và song song với cạnh còn lại thì sẽ tạo ra 1 tam giác mới và tam giác này sẽ đồng dạng với tam giác đã được cho trước.
Hệ quả 3
Hệ quả 3 của định lí Talet trong tam giác còn được biết đến là định lý Talet mở rộng. Người ta phát biểu định lý Talet mở rộng như sau: Khi ba đường thẳng đồng quy sẽ chắn trên 2 đường thẳng song song những cặp đoạn thẳng tỉ lệ.
Định lý Talet trong hình thang
Bên cạnh định lí Talet trong tam giác, chúng ta còn có thể áp dụng định lý này trong hình thang. Theo đó, định lý này được phát biểu như sau: Trong một hình thang, có một đường thẳng song song có cùng 2 cạnh đáy, đồng thời nó cắt 2 cạnh bên của hình thang đó thì sẽ định ra ở 2 cạnh bên đó những đoạn thẳng có tỷ lệ tương ứng với nhau.
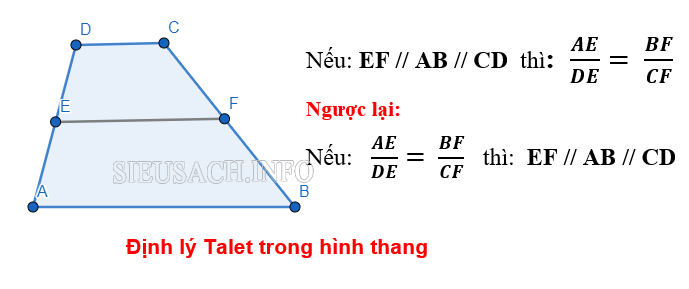
Định lý Talet trong hình thang
Ví dụ, khi cho một hình thang ABCD, điểm E sẽ thuộc đoạn AD, điểm F sẽ thuộc đoạn BC. Nếu như đoạn EF // AB // CD thì ta sẽ có AE/DE = BF/CF và ngược lại, trong hình thang ABCD, nếu ta có AE/DE = BF/CF thì EF // AB // CD.
Định lý Talet trong không gian
Định lý này cũng được ứng dụng đối với hình học không gian. Theo đó, định lý này trong không gian được phát biểu như sau: 3 mặt phẳng song song ở trong không gian sẽ chắn trên 2 đường thẳng những đoạn thẳng có một tỷ lệ tương ứng nhau.

Định lý ta-let trong không gian
Ngoài ra, người ta còn phát triển định lý đảo của định lý Talet trong không gian và định lý đảo được phát biểu như sau: 2 đường thẳng d1 và đường thẳng d2 chéo nhau, các điểm A1, B1, C1 ∈ (d1) và A2, B2, C2 ∈ (d2) và A1B1/B1C1 = A2B2/B2C2 thì những đường thẳng A1A2, B1B2, C1C2 sẽ cùng song song với một mặt phẳng.
Các dạng toán về định lý talet thường gặp
Dạng 1: Tính độ dài của đoạn thẳng, chu vi, diện tích và các tỉ số
Cách giải: sử dụng định lý talet, hệ quả của định lý talet và tỉ số đoạn thẳng để tính toán.
Ngoài ra ta còn sử dụng đến tính chất của tỷ lệ thức sau:
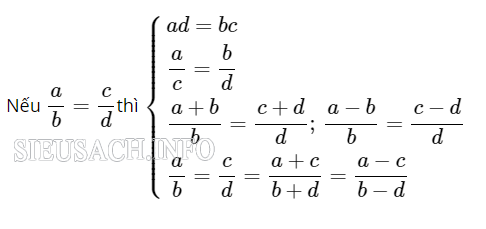
Dạng 2: Chứng minh hai đường thẳng song song, chứng minh các đẳng thức hình học.
Cách giải: sử dụng định lý Telet, định lý Talet đảo và hệ quả của định lý Talet để chứng minh nhé.
Bài tập áp dụng về định lý talet
Bài tập 1:Cho hình thang ABCD (AB // CD) AB < CD. Đường thẳng MN // với 2 đáy cắt cạnh AD, BC lần lượt tại M và N. Biết AD = 2cm, AM = 3cm, BC = 6cm. Tìm độ dài BN.
Giải: Vì hình thang ABCD có AB // CD // MN
Theo định lý Talet trong hình thang ABCD ta có,
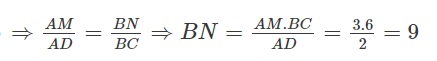
Bài tập 2 (Bài 9 trang 63/ SGK): Cho trước tam giác ABC và điểm D trên cạnh AB, sao cho đoạn thẳng AD = 13,5cm, đoạn thẳng BD = 4,5cm. Hãy tính tỉ số các khoảng cách từ D và B đến AC.
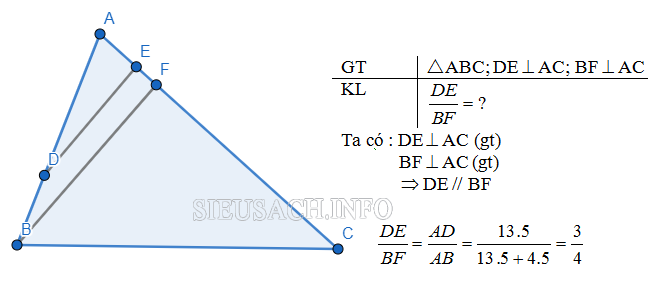
Bài tập 3 (bài 7 trang 62 / SGK):
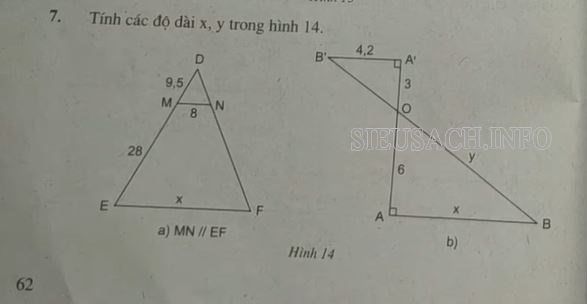
Lời giải:
 |
 |
Bài tập 4 (bài 10 trang 63 SGK):
ΔABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB , AC và đường cao AH theo thứ tự tại các điểm
B′ , C′ và H ′.

b, Áp dụng: Cho biết AH’ = 1/3 AH và diện tích tam giác ABC là 67,5 cm2. Tính diện tích tam giác AB’C’.

Bài tập 5: bài tập áp dụng định lý talet trong không gian

Ứng dụng của định lý Talet trong thực tiễn
Định lý Ta lét được ứng dụng vô cùng rộng rãi, đặc biệt khi đo đạc những kích thước quá lớn và chúng ta không thể trực tiếp đo được. Định lý Talet được ứng dụng trong 2 ví dụ sau:
- Đo đạc khoảng cách giữa 2 bờ sông mà không cần phải sang sông.
- Đo chiều cao của các vật dụng nhờ cách sử dụng bóng mặt trời.
Ngoài ra, định lí Talet cũng là công cụ quan trọng trong các lĩnh vực như: xây dựng, kiến trúc, địa chất, địa lý. Chẳng hạn như:
- Trong xây dựng các công trình kiến trúc, định lý talet được dùng để tính toán khoảng cách giữa các điểm
- Thiết kế chi tiết kết cấu: Các kỹ sư cần thiết kế các chi tiết kết cấu để đảm bảo tính chắc chắn và an toàn của công trình. Định lí Talet trong tam giác được áp dụng để tính toán các góc và khoảng cách giữa các điểm, giúp thiết kế các chi tiết kết cấu này chính xác.
- Trong địa chất học: Định lí Talet trong tam giác được sử dụng để tính toán các độ lệch địa chất và độ nghiêng của các lớp đất và đá.
- Đo đạc địa hình: Khi đo đạc địa hình, người ta sử dụng định lí Talet để tính toán khoảng cách và góc giữa các điểm.
- Xác định tọa độ: Định lí Talet trong tam giác còn được dùng để xác định tọa độ của các địa điểm và vị trí của vật thể trong không gian.
Như vậy, qua bài viết trên của chúng tôi, có thể thấy rằng định lí Talet trong tam giác chính là một phần rất quan trọng trong Toán học và nó được ứng dụng rộng rãi trong thực tế.




