Chúng ta đã được học định lý Menelaus trong chương trình toán lớp 9 và lớp 11. Để nắm chắc hơn về định lý này và ứng dụng nó vào việc giải toán bạn đọc đừng bỏ lỡ bài viết dưới đây nhé!
Định lý Menelaus
Định lý Menelaus chính là một định lý cơ bản trong hình học tam giác, phát biểu như sau: Cho tam giác ABC. Các điểm D, E, F lần lượt nằm trên các đường thẳng sau BC, CA, AB. Khi đó D, E, F thẳng hàng khi và chỉ khi:
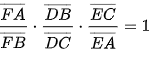
Ở đây ta nhận thấy rằng, nếu DBDC . ECEA . FAFB = 1 thì tùy theo số điểm nằm trên cạnh, đường thẳng chứa cạnh của tam giác mà ta có định lý Ceva hay Menelaus.
Nếu như cả 3 điểm D,E,F đều nằm trên ba cạnh của tam giác ABC thì chúng ta có định lý Ceva.
Nếu như có 2 điểm nằm trên cạnh và 1 điểm nằm trên phía đường thẳng chứa cạnh nhưng lại nằm ngoài tam giác ABC thì ta có định lý Menelaus.
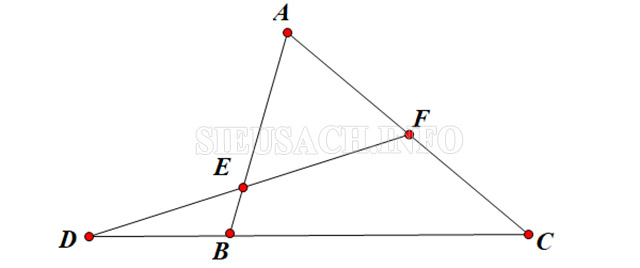
Định lý Menelaus là gì?
Nếu như có 1 điểm nằm trên cạnh và 2 điểm nằm phía trên đường thẳng chứa cạnh nhưng lại nằm ngoài tam giác ABC thì ta có định lý Ceva.
Nếu như cả 3 điểm D,E,F nằm trên ba đường thẳng chứa cạnh và nó nằm ngoài tam giác ABC thì chúng ta có định lý Menelaus.
Chứng minh định lí Menelaus
Phần thuận
Giả sử D, E, F là 3 điểm thẳng hàng với nhau. Hãy vẽ đường thẳng qua C và song song với AB và cắt đường thẳng DE tại G.
Vì CG//AB (c dựng) nên theo định lý Talet, chúng ta có:
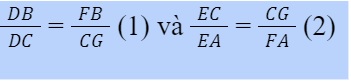
Nhân (1) và (2) và vế theo vế

Từ đó suy ra

Phần đảo

Khi đó ta gọi F’ là giao của đường thẳng ED với đường thẳng AB.
Theo chứng minh ở trên, ta có:

Kết hợp giả thuyết suy ra:

Nên F’A = FA và F’B = FB
Suy ra F’ trùng với F.
Vậy định lý đã được chứng minh.
Ví dụ về định lí menelaus:
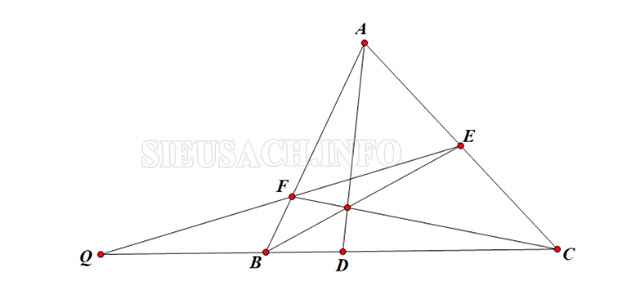
Cho tam giác ABC và ba điểm D, E, F nằm ở trên BC, CA, AB sao cho AD, BE, CF đồng quy. Đường thẳng EF sẽ cắt đường thẳng BC tại Q sao cho Q thuộc một nửa mặt phẳng bờ AD chứa B . Chứng minh rằng:

Ứng dụng định lý Menelaus trong giải toán
Bài 1: Cho tam giác ABC và ba điểm E, F, M trên các cạnh AC,BC,AB sao cho EF||BC và MB=MC. Chứng minh CF, BE, AM đồng quy.
Bài 2: Cho tam giác ABC vuông tại A, có đường cao AK. Dựng bên ngoài tam giác hai hình vuông là ABEF và ACGH. Chứng minh rằng CE, AK, BG đồng quy.
Bài 3: Cho tam giác ABC. Gọi M,N,P lần lượt là trung điểm của BC, CA, AB. Gọi X, Y, Z chính là ba điểm bất kì nằm trên BC, CA, AB để AX, BY, CZ đồng quy. Gọi D, E, F lần lượt làm trung điểm AX, BY, CZ. Chứng minh rằng PF, MD, NE đồng quy.
Bài 4: Cho tam giác ABC cùng đường tròn tâm I nội tiếp tam giác tiếp xúc với các cạnh AB, BC, CA lần lượt tại F, D, E. Gọi D′, E′, F′ lần lượt chính là điểm đối xứng của F, D, E qua I. Chứng minh rằng AD′,BE′,CF′ đồng quy.
Bài 5: Cho tam giác ABC. Đường tròn (O) cắt cạnh BC ở X,Y; cắt cạnh CA ở Z,T; cắt cạnh AB ở U,V sao cho XYZTUV chính là các đỉnh của một lục giác lồi. Lấy các giao điểm XT∩YU=A′; ZV∩TX=B′; UY∩VZ=C′. Chứng minh rằng AA′, BB′ và CC′ đồng quy với nhau.
Trên đây là các thông tin về định lý Menelaus trong không gian và cách ứng dụng định lý này vào giải toán. Hy vọng, bài viết đã cung cấp thêm cho bạn một nguồn tư liệu để bạn dạy và học tốt hơn.




