Định lý Cosin trong tam giác là một định lý rất quan trọng, được ứng dụng rộng rãi trong chương trình giáo dục đào tạo. Bài viết dưới đây là những kiến thức tổng hợp về định lý Cosin, mời bạn đọc cũng theo dõi.
Sự ra đời của định lý Cosin
Nhà toán học Al Kashi
Nhà toán học Al Kashi là người phát minh ra định lý Cosin. Ông là một nhà thiên văn học, toán học của vùng Trung Á và là một trong những nhà bác học lớn của trường phái Samarkand đầu thế kỷ XV. Do đó, trong nhiều tài liệu người ta còn ghi định lý Cosin là định lý Al Kashi.

Định lý Cosin chính là mở rộng của định lý Pythagore. Nếu như định lý Pythagore cung cấp cho chúng ta một công cụ để tìm một cạnh còn thiếu trong một tam giác vuông, định lý hàm số Cosin lại đưa ra một phương pháp giúp chúng ta tìm được một cạnh của tam giác thường khi đã biết được hai cạnh và góc xen giữa chúng, các góc của một tam giác khi đã biết các cạnh của một tam giác, cạnh thứ ba của một tam giác nếu như biết hai cạnh và góc đối của một trong hai cạnh đó.
Định lý hàm Cosin trong tam giác

Định lý Cosin trong tam giác
Định lý Cosin
Định lý Cosin lớp 10 bằng lời như sau: Trong một tam giác, bình phương một cạnh sẽ bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.
Trong tam giác ABC, với AB = c, BC = a, AC = b chúng ta có:
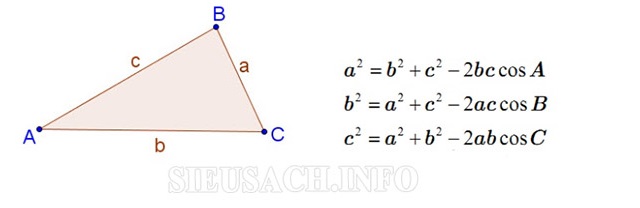
Như vậy, trong một tam giác nếu như biết được hai cạnh và góc xen giữa chúng ta sẽ tính được độ dài của cạnh còn lại.
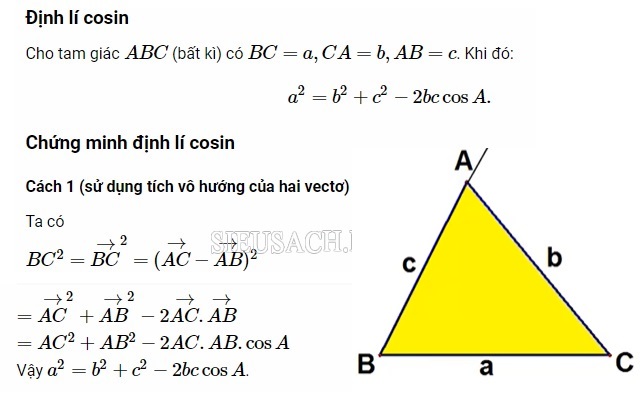
Chứng minh định lý Cosin
Để chứng minh định lý Cosin chúng ta có thể áp dụng cách dưới đây:
Hệ quả định lý Cosin
Từ định lý hàm số Cosin chúng ta có thể dễ dàng suy ra được các biểu thức tính giá trị cosA, cosB, cosC theo 3 cạnh của tam giác ABC:
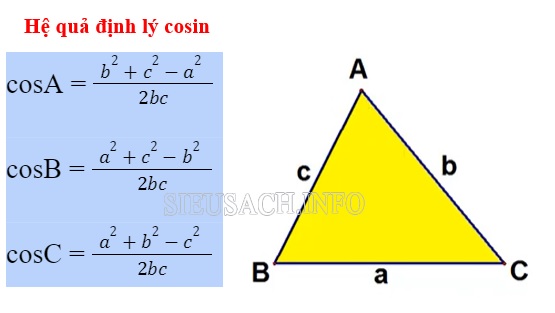
Hệ quả 1 định lý cosin
Như vậy hệ quả của định lý cosin cho thấy, nếu như biết được độ dài của 3 cạnh chúng ta sẽ tính được số đo của các góc. Hoặc có thể hiểu đơn giản, định lý cosin sẽ giúp chúng ta tính được độ dài của cạnh, hệ quả của định lý này sẽ giúp ta tính được số đo của góc.
Bên cạnh đó, việc áp dụng định lý hàm số Cosin sẽ giúp chúng ta tìm được độ dài các đường trung tuyến theo 3 cạnh của một tam giác. Cụ thể như sau:
Trong tam giác ABC, có AB = c, BC = a, AC = b. Nếu như đặt các đường trung tuyến kẻ từ các đỉnh A, B, C lần lượt là ma , mb , mc thì ta có:
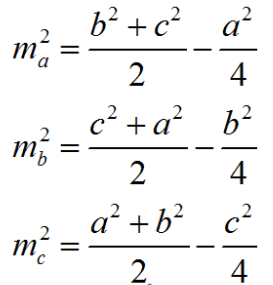
Hệ quả 2 định lý cosin trong tam giác
Với ha, hb, hc lần lượt là độ dài đường cao kẻ từ A, B, C ta có một số công thức tính diện tích tam giác như sau:
Cách vận dụng định lý Cosin trong tam giác cân
Ví dụ. Cho tam giác ABC, ta có AB = c, BC = a, CA = b và M chính là trung điểm của BC. Hãy tính độ dài đường trung tuyến AM theo a, b và c.
Phân tích:
– Bài toán yêu cầu ta tính độ dài một đoạn thẳng AM, nguyên tắc dùng để tính đoạn thẳng đó là xem nó là một cạnh của một cạnh của tam giác nào đó.
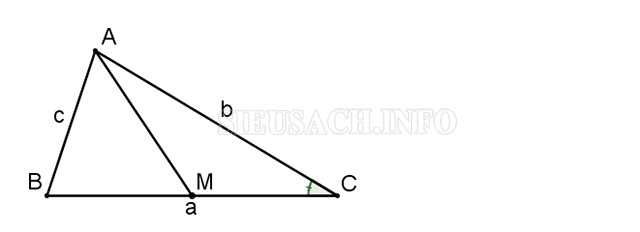
– Theo đề bài, chúng ta sẽ có 2 lựa chọn, xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của các tam giác này là ngang nhau nên ta chúng chọn tam giác nào cũng được. Ở đây chúng ta chọn tam giác ACM.
– Xét tam giác ACM theo nguyên tắc chung, để tính được cạnh AM chúng ta cần biết hai cạnh còn lại đó là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC = b theo như giả thiết, còn CM = a/2 do M là trung điểm của BC, nhưng ta lại chưa biết góc C. Như vậy, nếu như tính được góc C thì AM sẽ tính được nhờ vào định lý Cosin.
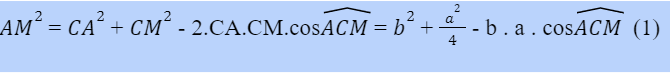
– Nhận xét rằng, muốn tính được góc trong tam giác chúng ta cần biết ba cạnh của tam giác đó. Vì vậy không thể xét tam giác ACM để tính góc C, vì tam giác này còn thiếu cạnh AM mà ta cần tính.
– Nhưng, ta thấy rằng góc C của tam giác ACM cũng chính là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vì vậy áp dụng hệ quả của định lý Cosin chúng ta sẽ tính được góc C.

– Thay (2) vào (1), rồi rút gọn ta cho ra kết quả
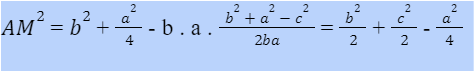
Bài tập áp dụng về định lý cosin trong tam giác
Bài 1: Đường dây cao thế thẳng từ vị trí A đến vị trí B dài 10km, từ vị trí A đến vị trí C dài 8km, góc tạo bởi hai đường dây trên khoảng 75° độ. Tính khoảng cách từ vị trí B đến vị trí C?
Giải: Theo định lý cosin ta có: a² = b² + c² – 2.b.c.cosA = 8² + 10² – 2.8.10.cos75° ≈ 122 km
Vậy khoảng cách từ B đến C là 11 km
Bài 2: Cho tam giác ABC có cạnh BC = a, cạnh CA = b, cạnh AB = c và đường trung tuyến AM = c = AB. Chứng minh rằng: a² = 2.(b² + c²)?
Giải: – theo định lý về trung tuyến của tam giác ta có:
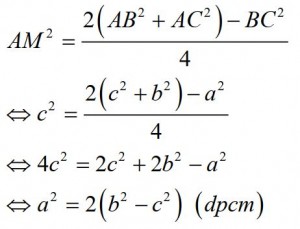
Bài 3: Cho tam giác ABC có góc A=120°, cạnh b=8cm và c=5cm. Tính cạnh a và các góc B, C của tam giác đó?
-Theo định lý cosin ta có: a² = b² + c² – 2.b.c.cosA = 8² + 5² – 2.8.5.cos120° => a ≈ 11,4 km
-CosB = (c² + a² – b²) / 2.a.c => góc B ≈ 37° độ
-Góc: A + B + C = 180° => góc C = 180° – 120° – 37° = 23° độ
Bài 4: Cho tam giác ABC có AB = 4, BC= 9, AC = 7
a) Tính số đo góc B
b) gọi M là trung điểm của AB, N thuộc cạnh BC sao cho BN = 2NC. Tính MN
Giải:

Vậy là bài viết trên đã giải đáp rõ về định lý Cosin và cách vận dụng định lý Cosin trong tam giác. Hy vọng bài viết sẽ giúp bạn hiểu rõ định lý này hơn và áp dụng chúng vào các bài tập một cách hiệu quả.





