Hình thang cân là kiến thức quan trọng được học trong môn Toán 8 ở chương trình THCS. Vậy, hình thang cân là gì? Hình thang cân có tính chất gì, công thức tính chu vi, diện tích như thế nào? chuthapdoquangninh.org.vn sẽ giải đáp thắc mắc của quý bạn đọc trong bài dưới đây.
Hình thang cân là gì?
Hình thang cân là một tứ giác có hai nằm cạnh song song (trong hình thang) và có hai góc nằm kề một cạnh đáy bằng nhau.
Ví dụ: Tứ giác ABCD là hình thang cân với 2 đáy là AB, CD <=> AB // CD và 2 góc đáy kề nhau góc C = góc D
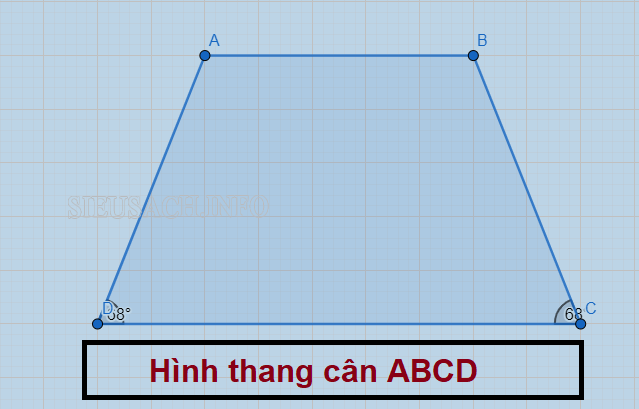
Tứ giác ABCD là hình thang cân
Tính chất hình thang cân
Cho hình thang ABCD, có cạnh AB//CB, thì:
- Định lý 1: Hình thang cân có 2 cạnh bên độ dài bằng nhau ( AD = BC )
- Định lý 2: Hình thang cân có 2 góc kề cạnh đáy bằng nhau ( góc C = góc D; góc A = góc B)
- Định lý 3: Hình thang cân có 2 đường chéo bằng nhau (AC = DB)
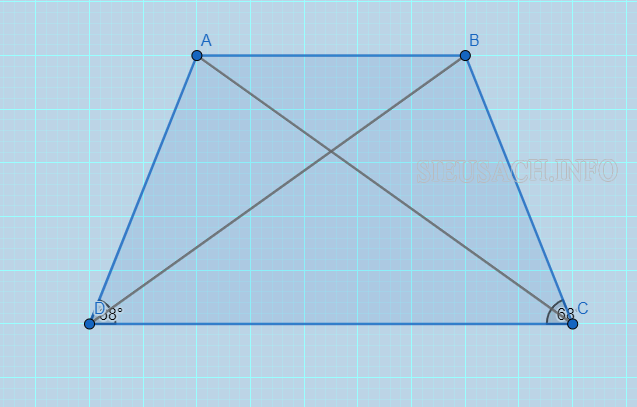
Tính chất hình thang cân ABCD
Bên cạnh đó, hình thang cân có đường tròn nội tiếp với 4 điểm của hình thang đều thuộc đường tròn đó.
Các dấu hiệu nhận biết và cách chứng minh hình thang cân
Cách dấu hiệu nhận biết một hình thang cân
- Hình thang có hai đường chéo có độ dài bằng nhau là hình thang cân.
- Hình thang có hai góc kề ở một cạnh đáy bằng nhau đó là hình thang cân.
- Hình thang là nội tiếp của một đường tròn là hình thang cân.
- Hình thang có 2 trục đối xứng của 2 đáy trùng nhau đó là dấu hiệu của hình thang cân.
- Hình thang có 2 cạnh bên bằng nhau và 2 cạnh bên đó không nằm song song thì đó là một hình thang cân.
Ví dụ: Trong ta xét tứ giác ABCD và EFGH trên giấy có các đường kẻ ô vuông ở hình dưới đây thì tứ giác nào là hình thang cân? Giải thích vì sao?
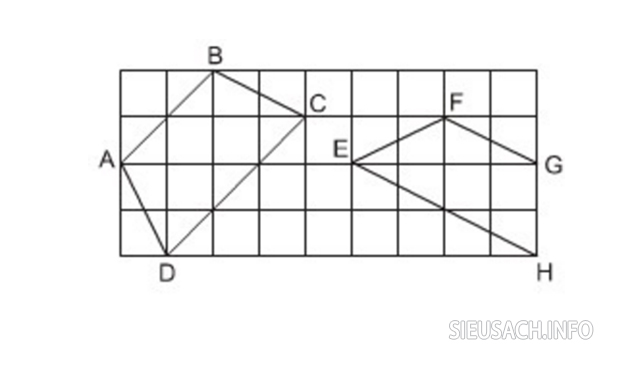
Hình vẽ tứ giác ABCD và EFGH
Lời giải:
Dựa vào các dấu hiệu nhận biết hình thang cân ở trên ta có thể dễ dàng so sánh bằng mắt thường về độ dài của các cạnh bên. Theo đó:
Trong tứ giác ABCD có cạnh AD = BC thì đây là một hình thang cân.
Tứ giác EFGH có cạnh EF > GH nên tứ giác này không phải là hình thang cân.
Cách chứng minh hình thang cân
Để chứng minh được một tứ giác là hình thang cân, chúng ta có thể dựa theo các phương pháp dưới đây.
Phương pháp 1:
Để chứng minh tứ giác là hình thang cân thì cần chứng minh tứ giác đó có 2 cạnh song song dựa vào:
– Hai góc ở vị trí so le trong hình tứ giác bằng nhau.
– Hai góc đồng vị bằng nhau.
– Hai góc trong cùng phía bù nhau hoặc dựa vào định lý từ góc vuông đến góc song song.
Cách chứng minh hình thang cân trong toán lớp 8
Phương pháp 2:
Chứng minh hình thang có 2 góc kề với một đáy bằng nhau → đó là hình thang cân.
Phương pháp 3:
Chứng minh hình thang đó có 2 đường chéo có độ dài bằng nhau → Kết luận đó là hình thang cân (Đây cũng là phương pháp thường được sử dụng khi gặp các bài tập về chứng minh hình thang cân).
Công thức tính diện tích hình thang cân
Diện tích hình thang cân được áp dụng như với công thức tính diện tích hình thang thông thường. Do đó ta có công thức như sau:
S = (h.(a+b))/2
Trong đó:
- S là ký hiệu diện tích hình thang
- h là ký hiệu chiều cao của hình thang
- a, b là độ dài 2 đáy
Công thức tính chu vi hình thang cân
Giả sử ta có hình thang ABCD (AB//CD) là hình thang cân có độ dài hai cạnh đáy lần lượt là a, b và độ dài cạnh bên là c.
Khi đó, ta có công thức tính chu vi hình thang ABCD là:
P = a + b + 2c
Ứng dụng thực tế của hình thang cân trong đời sống
Hình thang cân là 1 hình dạng phổ biến thường gặp trong cuộc sống. Chúng ta thường bắt gặp hình dạng này trong các đồ chơi trẻ em. Bên cạnh đó, hình thang cân còn được tạo thành các mô hình bằng nhiều chất liệu khác nhau để các em học sinh có thể nhận biết và học tập.
Trong thực tế, chúng ta cũng có thể thấy hình ảnh hình thang cân trong các vật dụng hàng ngày như túi xách, chiếc thang, thùng đựng rác….
Các dạng bài tập về hình thang cân lớp 8
Dạng 1. Tính số đo góc, độ dài cạnh và diện tích hình thang cân
Phương pháp giải: Sử dụng tính chất hình thang cân về cạnh góc, đường chéo và công thứ tính diện tích hình thang để tính toán.
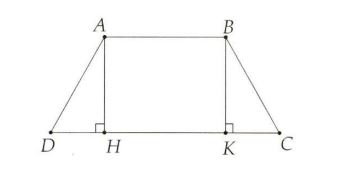
Bài tập 1: Cho hình thang cân ABCD (AB // CD) có AH và BK là hai đường cao của hình thang
a) Chứng minh DH = (CD – AB)/2
b) Biết AB = 6 cm, CD = 14 cm, AD = 5 cm, tính DH, AH và diện tích hình thang cân ABCD.
Giải:
 |
Giải:
a) ABCD là hình thang cân nên: AD = BC và Góc ADH = góc BCK b) ΔADH vuông tại H, có AD = 5, DH = 4. Theo định lý Pytago thì : AH2 = AD2 – DH2 => AH = 3cm; SABCD = AH . ( AB + CD)/2 = 3. (14 +6)/2 = 30cm2 |
Bài tập 2: Cho hình thang cân ABCD (AB//CD) có góc A = góc B = 60° , AB = 4,5cm; AD = BC = 2 cm. Tính độ
dài đáy CD và diện tích hình thang cân ABCD
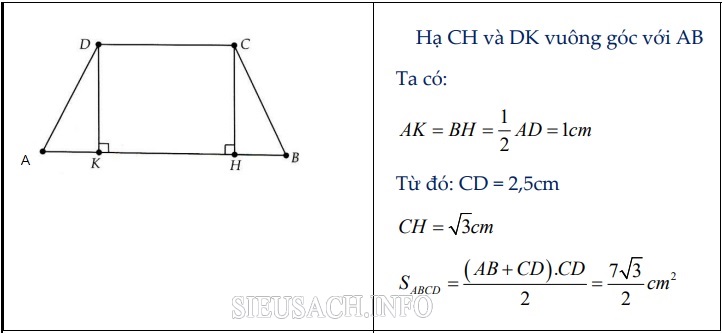
Dạng 2. Chứng minh hình thang cân
Phương pháp giải: Sử dụng các dấu hiệu nhận biết hình thang cân.
Bài tập 1:
Cho hình thang ABCD (AB // CD) trong đó cho góc ACD = góc BDC. Hãy chứng minh rằng hình thang ABCD trên là một hình thang cân.
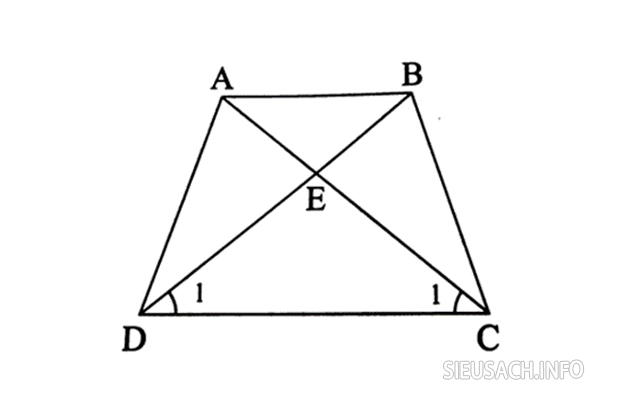
Lời giải:
Bài tập 2:
Cho tam giác ABC cân tại A. Trên cạnh AB và AC lấy theo thứ tự các điểm D, E sao cho AD = AE.
- a) Chứng minh rằng tứ giác BDEC là hình thang cân
- b) Biết góc A = 50 độ hãy tính các góc còn lại của hình thang cân đó.
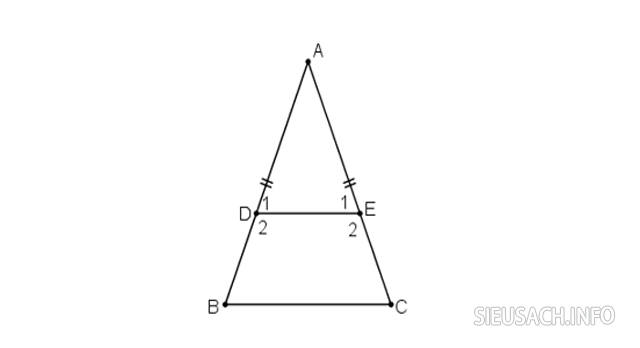
Lời giải:

Dạng 3: Chứng minh các cạnh bằng nhau, các góc bằng nhau trong hình thang cân
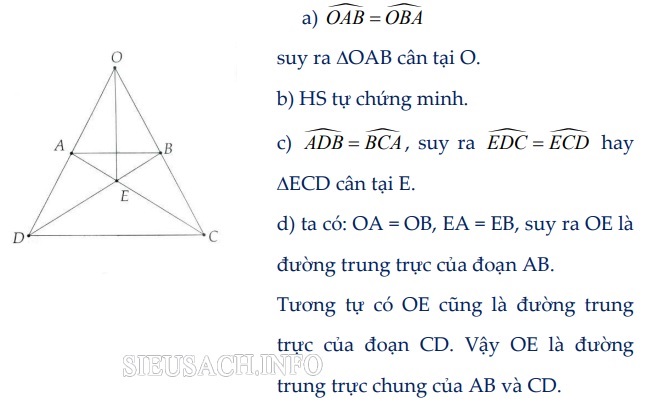
Bài 1: Cho hình thang cân ABCD (AB // CD, AB < CD ). Gọi O là giao điểm của AD và BC; Gọi E là giao điểm của AC và BD. Chứng minh:
a) Tam giác AOB cân tại O;
b) ΔABD = ΔBAC;
c) EC = ED;
d) OE là trung trực chung của AB và CD.
Giải:
Bài 2: Cho tam giác ABC cân tại A và điểm M tùy ý nằm trong tam giác. Kẻ tia Mx song song với BC cắt AB ở D, tia My song song với AC cắt BC ỏ E. Chứng minh:
![]()
Giải: 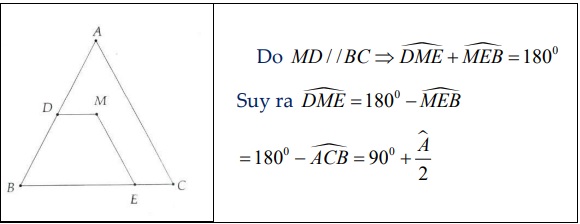
Trên đây là toàn bộ bài viết của chuthapdoquangninh.org.vn về hình thang cân là gì và những thông tin liên quan đến hình thang cân. Hy vọng bài viết đã giúp bạn hiểu và nắm vững hơn về phần kiến thức toán học này. Chúc bạn đạt được nhiều điểm cao trong môn học Toán nhé.




